10 月 11 日消息,南京大学类脑智能科技研究中心研究团队提出了一种高精度模拟存内计算方案,并以此为基础,研发出一款基于互补金属氧化物半导体工艺的模拟存算一体芯片。
该方案将模拟计算权重的实现方式从不稳定、易受环境干扰的物理参数(例如器件电阻)转向高度稳定的器件几何尺寸比,突破了限制模拟计算精度的瓶颈。
测试数据表明,该芯片在并行向量矩阵乘法运算中实现了仅 0.101% 的均方根误差,创下了模拟向量-矩阵乘法运算精度的最高纪录。相关成果已于 9 月 12 日刊发于国际学术期刊《科学・进展》。

据介绍,该芯片在-78.5°C 和 180°C 的极端环境下依然能稳定运行,矩阵计算的均方根误差分别维持在 0.155% 和 0.130% 的水平,展现出在极端环境下保持计算精度的优秀能力。不仅如此,该方案还可应用于各种二值存储介质,因而具备广泛的应用潜力。
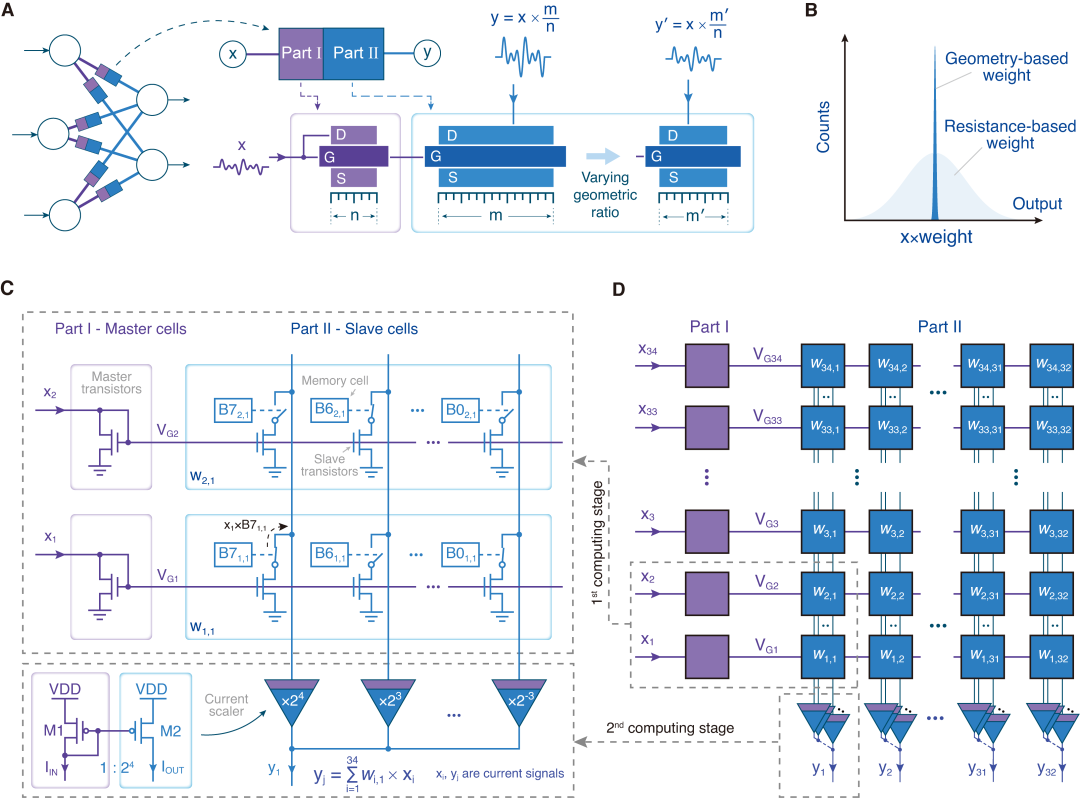
▲ 图 1:高精度模拟计算方案与电路结构。(A) 概念示意图。本方案利用器件的物理尺寸决定模拟信号的运算关系。(B) 实现效果示意图。利用器件物理尺寸的稳定性,本方案可实现超越传统方案的计算精度。(C) 计算单元原理图。通过两级依赖尺寸比例的电流拷贝电路设计,结合存储单元和开关器件,构建了等效尺寸比例可编程的计算单元,实现输入电流与 8 比特权重的模拟乘法运算。(D) 计算阵列原理图。通过阵列化排布计算单元,设计高精度电流域向量-矩阵乘法芯片。
本研究的核心思想是将模拟计算权重的实现方式从器件参数转向器件的几何比例(图 1A),利用器件几何比例在制备完成后具备极高稳定性的特点,实现高精度计算(图 1B)。基于这一思想,研究团队通过电路拓扑设计,结合存储单元和开关器件,构建了可编程的计算单元(图 1C)。该单元通过两级依赖尺寸比例的电流拷贝电路实现输入电流与 8 比特权重的乘法运算:第一级的几何比例由 8 位存储器控制;第二级为固定比例,为不同列上的第一级输出电流赋予对应的二进制权重。两级共同作用,决定计算单元的整体等效比例,从而实现权重可编程的模拟乘法运算。通过阵列化排布这些计算单元,研究团队设计出了一款高精度电流域向量-矩阵乘法芯片(图 1D)。
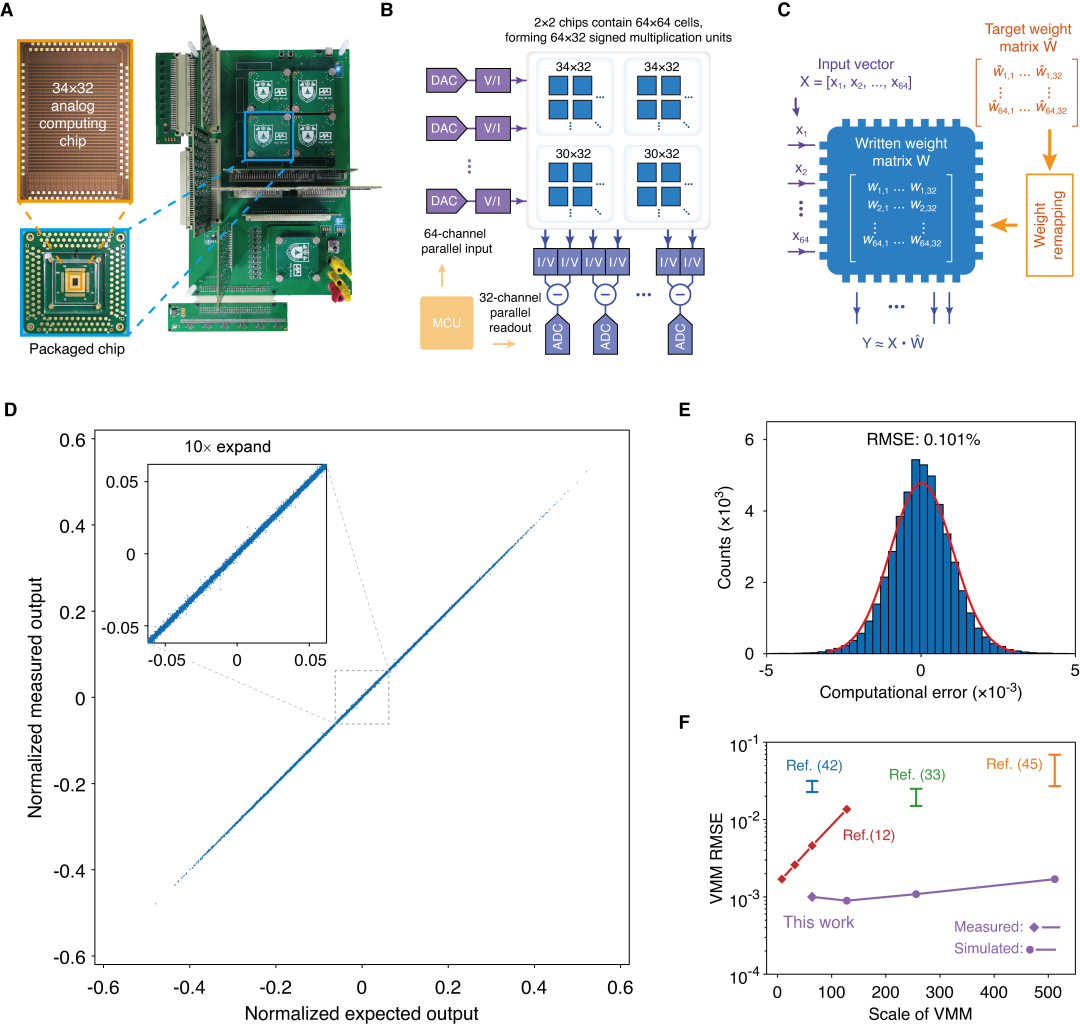
▲ 图 2:高精度模拟向量-矩阵乘法测试。(A) 芯片和测试电路照片。(B) 模拟向量-矩阵乘法精度测试电路原理图。(C) 权值重映射方法示意图。该方法能进一步提高芯片计算精度。(D) 1500 组随机向量-矩阵乘法结果。理想输出与实际输出几乎重合。(E) 归一化计算误差的分布图,统计得其均方根仅为 0.101%。(F) 本芯片与其他先进模拟计算方案的精度对比。
随后,研究团队基于 180 nm CMOS 工艺对该方案进行了流片验证。芯片照片与测试电路如图 2A 所示。研究团队通过执行多轮随机向量-矩阵乘法充分测试了该芯片的计算精度。测试使用的矩阵规模为 64×32(图 2B),总共由 4 块芯片组成。同时,研究团队提出了一种权值重映射方法(图 2C),可以最大程度利用器件尺寸比例的稳定性,从而进一步提高芯片的计算精度。在 1500 次随机向量-矩阵乘法实验中,测量到的芯片输出结果与理想值几乎完全一致(图 2D),体现出极高的计算精度。进一步的统计结果显示,芯片计算相对误差的均方根仅为 0.101%(图 2E),刷新了模拟计算领域的最高精度纪录。与其他模拟计算方案相比,本芯片的计算精度显著提高(图 2F)。
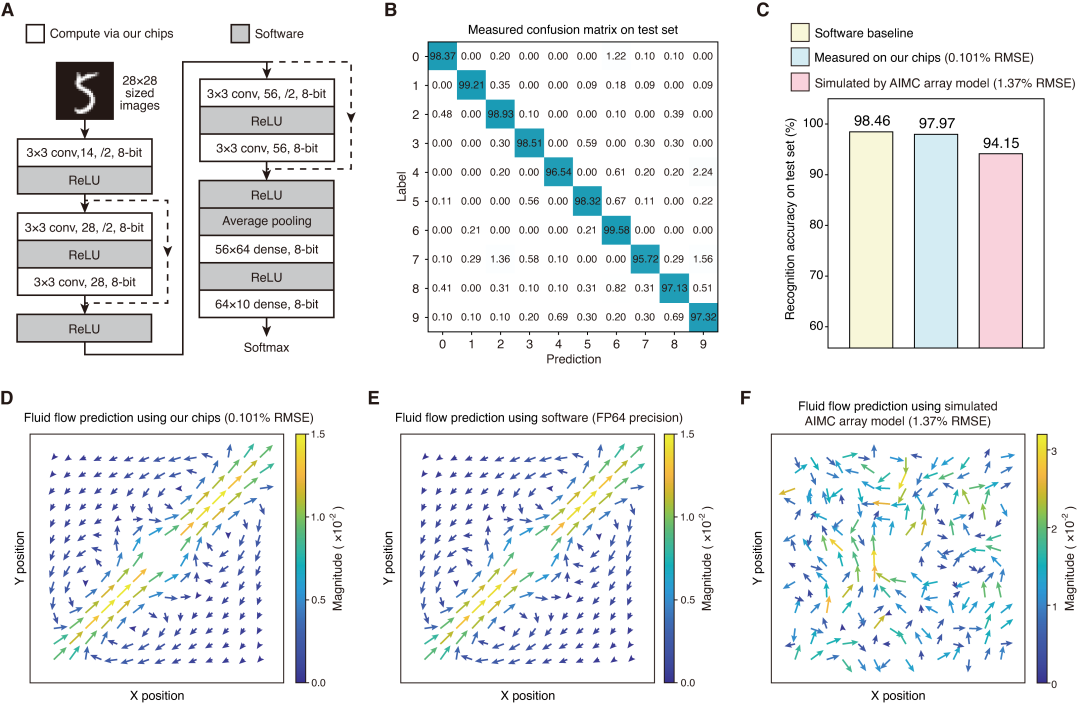
▲ 图 3:高精度模拟计算芯片的应用表现。(A) 神经网络结构与数据集。(B) 在 MNIST 测试集上识别结果的混淆矩阵,识别率达到 97.97%。(C) 准确率对比。高精度模拟计算芯片测试结果与 64 位浮点精度下的软件识别率相近(-0.49%),显著优于传统模拟计算硬件(+3.82%)。(D) 高精度模拟计算芯片求解纳维–斯托克斯方程得到的流体行为预测结果。(E) 64 位浮点精度下的软件计算结果,本芯片结果与其高度一致。(F) 低精度模拟计算硬件的结果无法准确反映流体行为。
该芯片具有的超高模拟向量-矩阵乘法精度,使得其在实际应用中表现优异。研究团队首先测试了芯片在神经网络推理任务中的应用效果:利用团队研发的高精度模拟存算芯片执行图 3A 所示神经网络中的全部卷积层和全连接层运算时,在 MNIST 测试集上识别准确率达到 97.97%(图 3C),这与 64 位浮点精度下的软件识别率相近(-0.49%),显著优于传统模拟计算硬件(+3.82%)。进一步,团队测试了该芯片在科学计算应用中的表现。研究团队利用高精度模拟存算芯片求解纳维–斯托克斯方程,以模拟流体流动行为。经实验测试,芯片计算出的流体运动结果(图 3D)与 64 位浮点精度的结果高度一致(图 3E),而传统低精度模拟计算硬件在执行相同任务时则无法得到正确的结果(图 3F)。
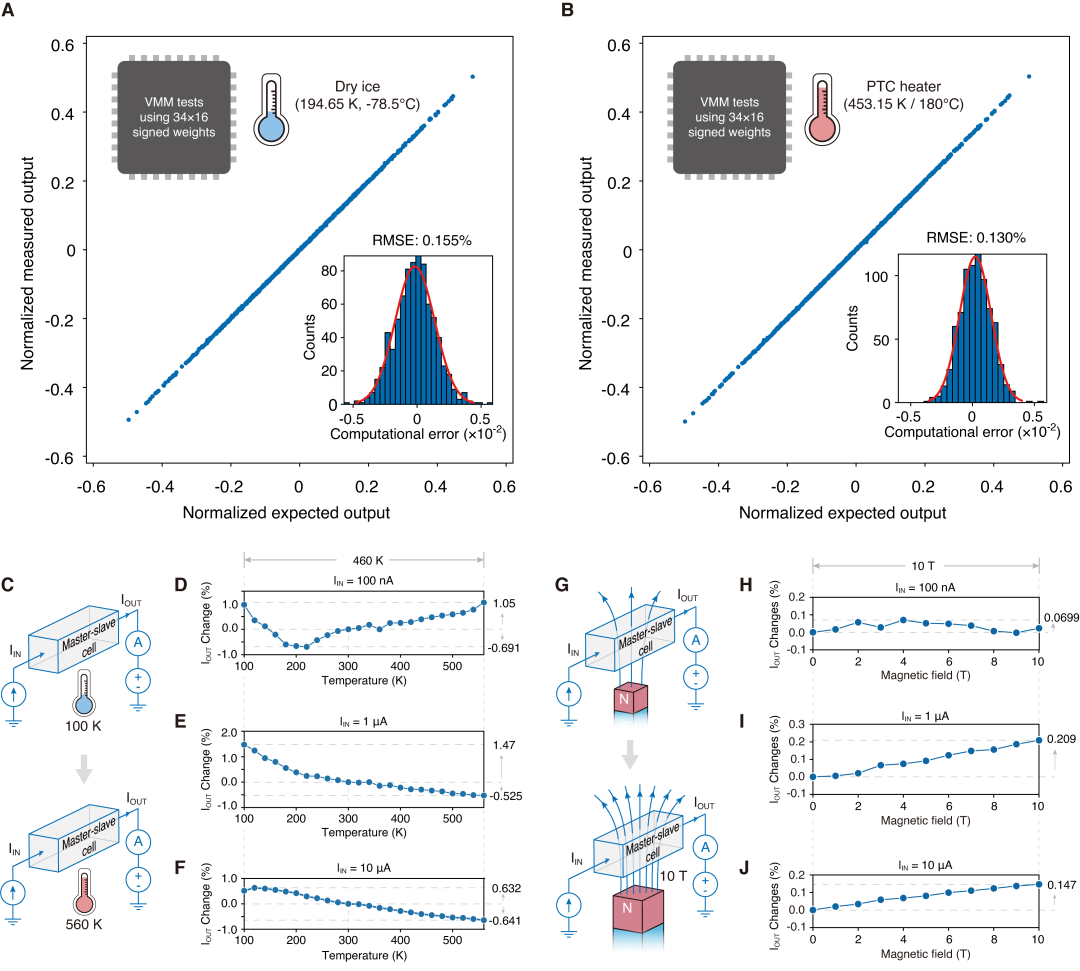
▲ 图 4:高精度模拟计算芯片的鲁棒性测试。(A) 低温下(-78.5℃)芯片的向量-矩阵乘法精度测试结果。测得芯片输出的相对误差均方根为 0.155%。(B) 高温下(180℃)芯片的向量-矩阵乘法精度测试结果。测得芯片输出的相对误差均方根为 0.130%。(C) 将芯片核心单元置于更宽温区(-173.15℃至 286.85℃)进行测试的示意图。(D)-(F) 宽温区下的输出电流测量结果。相对于常温条件,输出电流偏差不超过 1.47%。(G) 将芯片核心单元置于强磁场(最高 10 T)下进行精度测试的示意图。(H)-(J) 强磁场下的输出电流测量结果。相对于零磁场条件,输出电流偏差不超过 0.21%。
研究团队不仅测试了该模拟存算芯片的超高计算精度,还验证了这一芯片在极端环境中有效保持计算精度的鲁棒性。即使在外界环境变化条件下,器件的几何比例依然能保持恒定,这使得本芯片在极端环境中仍然能保持较高的计算精度。研究团队在-78.5℃和 180℃下利用该模拟存算芯片执行模拟向量-矩阵乘法运算测试,测得相对误差的均方根分别仅为 0.155% 和 0.130%(图 4A、B)。在更宽温区(-173.15℃至 286.85℃)的测试中,芯片核心单元输出电流相较于常温条件的最大偏差仅为 1.47%(图 4C-F)。此外,研究团队也在强磁场环境(最高 10 T)中对芯片输出电流进行了测量。结果显示,芯片核心单元的输出电流相较于无磁场条件的变化不超过 0.21%(图 4G-J)。上述结果充分说明了团队所提出的高精度模拟计算方案在极端环境下的可靠性。
