引言:从系统架构到可重现性保证
区块链系统传统上依赖哈希运算确保安全,而Gonka PoW 2.0创新性地将大语言模型引入工作量证明。本文揭示其如何通过种子机制与确定性算法,在保证计算结果不可预测的同时,确保全网节点可验证计算过程。
在深入了解具体的技术实现之前,我们需要先理解PoW 2.0系统架构的整体设计,以及可重现性在其中扮演的关键角色。
1. PoW 2.0系统架构概览
1.1 分层架构设计
Gonka PoW 2.0采用分层架构,确保可重现性从区块链层面贯穿到计算执行层面: 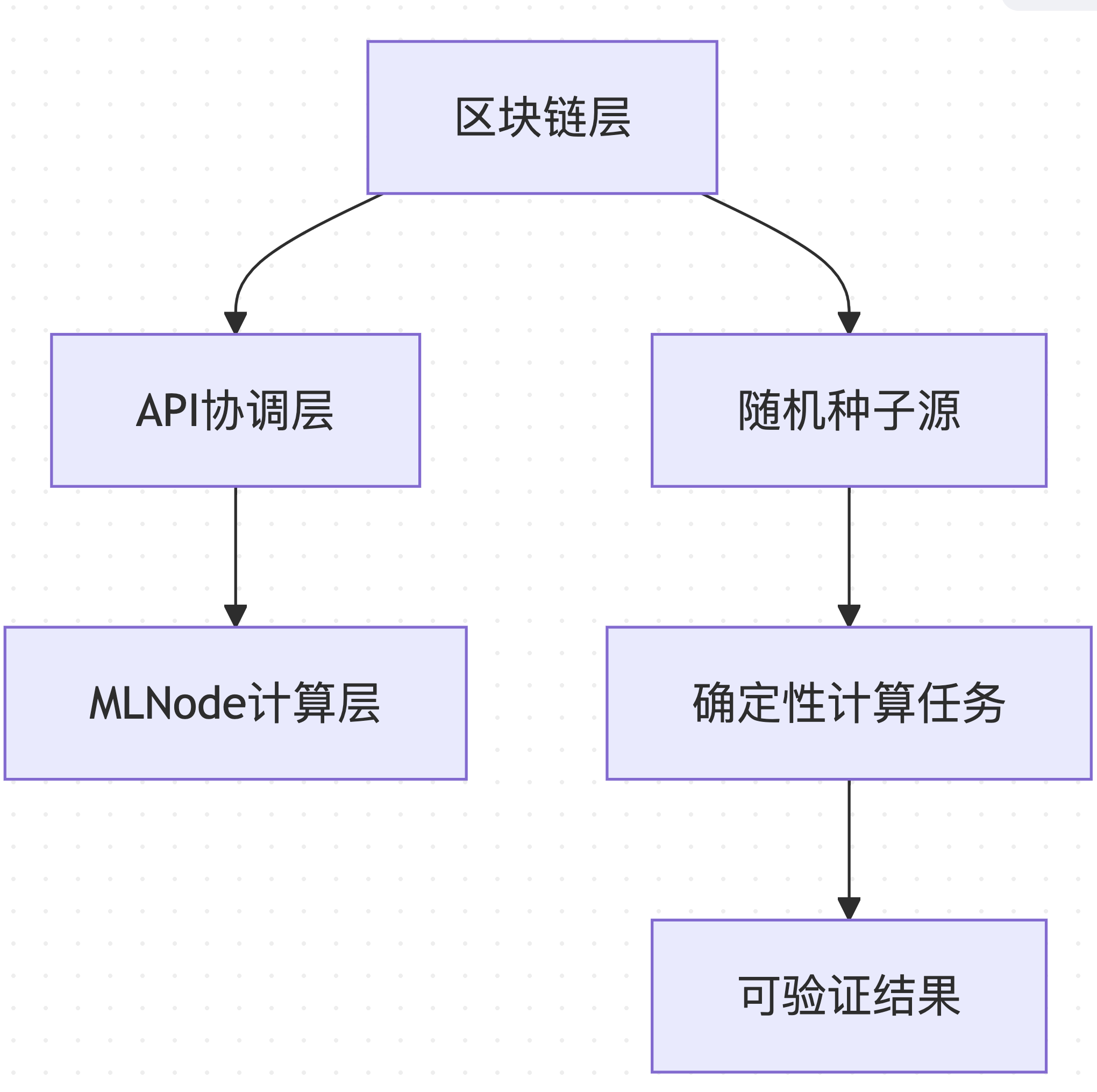
数据来源 :基于 decentralized-api/internal/poc 和 mlnode/packages/pow 的架构设计
这种分层设计使得系统的不同组件可以独立优化,同时保持整体的一致性和可验证性。
1.2 可重现性的核心目标
PoW 2.0系统的可重现性设计服务于以下核心目标:
1. 计算公平性 :确保所有节点面临相同的计算挑战
2. 结果验证性 :任何诚实节点都能重现和验证计算结果
3. 防作弊保证 :使预计算和结果伪造在计算上不可行
4. 网络同步 :确保分布式环境下的状态一致性
这些目标共同构成了PoW 2.0可重现性设计的基础,确保了系统的安全性和公平性。
2. 种子系统:多层次随机性的统一管理
在了解了系统架构之后,我们需要深入探讨实现可重现性的关键技术——种子系统。这个系统通过多层次的随机性管理,确保了计算的一致性和不可预测性。
2.1 种子类型与特定目标
Gonka PoW 2.0设计了四种不同类型的种子,每种服务于特定的计算目标:
网络级种子(Network-Level Seeds)
数据来源 :decentralized-api/internal/poc/random_seed.go#L90-L111 
目标 :为整个网络的每个epoch提供统一的随机性基础,确保所有节点使用相同的全局随机源。
网络级种子是整个系统随机性的根基,通过区块链交易确保全网节点使用相同的随机性基础。
任务级种子(Task-Level Seeds)
数据来源 :mlnode/packages/pow/src/pow/random.py#L9-L21 
目标 :通过多轮SHA-256哈希扩展熵空间,为每个计算任务生成高质量的随机数生成器。
任务级种子通过扩展熵空间,为每个具体的计算任务提供高质量的随机性。
节点级种子(Node-Level Seeds)
数据来源 :种子字符串构造模式 `f"{hash_str}_{public_key}_nonce{nonce}"`
目标 :确保不同节点和不同nonce值产生完全不同的计算路径,防止碰撞和重复。
节点级种子通过结合节点公钥和nonce值,确保每个节点的计算路径都是唯一的。
目标向量种子(Target Vector Seeds)
数据来源 :mlnode/packages/pow/src/pow/random.py#L165-L177

目标 :为整个网络生成统一的目标向量,所有节点都朝着相同的高维球面位置进行优化。
目标向量种子确保全网节点朝着相同的目标进行计算,这是验证结果一致性的关键。
2.2 种子生命周期管理 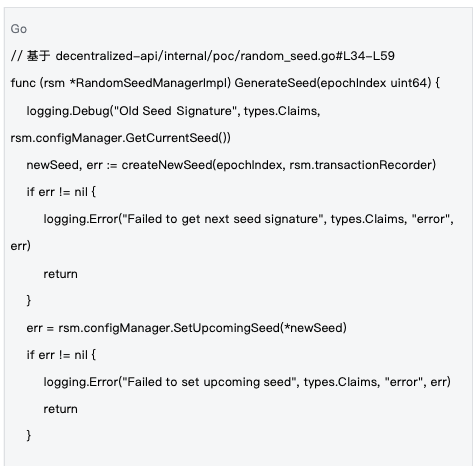
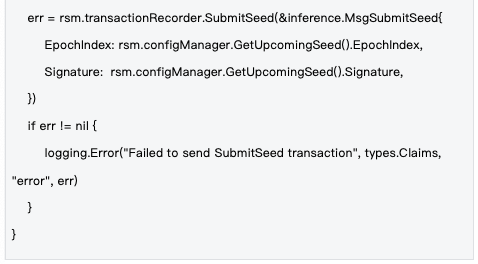
管理机制 :种子在epoch级别进行管理,每个epoch开始时生成新种子,通过区块链交易同步到全网,确保所有节点使用相同的随机性基础。
种子的生命周期管理确保了随机性的时效性和一致性,是系统安全运行的重要保障。
3. LLM组件的种子驱动生成机制
在了解了种子系统之后,我们需要进一步探讨如何将这些种子应用到LLM组件的生成过程中。这是实现可重现性的关键环节。
3.1 模型权重的随机初始化
为什么需要随机初始化模型权重?
在传统的深度学习中,模型权重通常通过预训练获得。但在PoW 2.0中,为了确保:
1. 计算任务的不可预测性 :相同的输入不会因为固定权重而产生可预测的输出
2. ASIC抗性 :专用硬件无法针对固定权重进行优化
3. 公平竞争 :所有节点使用相同的随机初始化规则
数据来源 :mlnode/packages/pow/src/pow/random.py#L71-L88 
随机初始化模型权重是确保计算不可预测性和公平性的关键步骤。
权重初始化的确定性过程
数据来源 :mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125 
关键特性 :
• 使用区块哈希作为随机种子,确保所有节点生成相同的权重
• 采用正态分布 N(0, 0.02²) 进行权重初始化
• 支持不同的数据类型(如float16)进行内存优化
这种确定性过程确保了不同节点在相同条件下生成完全一致的模型权重。
3.2 输入向量生成机制
为什么需要随机输入向量?
传统PoW使用固定的数据(如交易列表)作为输入,但PoW 2.0需要为每个nonce生成不同的输入向量,确保:
1. 搜索空间的连续性 :不同nonce对应不同的计算路径
2. 结果的不可预测性 :输入的微小变化导致输出的巨大差异
3. 验证的高效性 :验证者可以快速重现相同的输入
数据来源 :mlnode/packages/pow/src/pow/random.py#L129-L155 

随机输入向量的生成确保了计算的多样性和不可预测性。
输入生成的数学基础
数据来源
